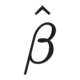The Battle for the Soul of Causal Inference: Pearl vs. Rubin
In causal inference methodology, an intellectual battle of titans has been unfolding for decades. This conflict isn’t merely academic - it represents fundamentally different ways of conceptualizing causality, with major implications for how researchers approach causal questions across disciplines.
This blog is based on a guest lecture delivered on March 20, 2025, in PBHLT 7115 - Causal Methods in Public Health at the University of Utah. It is based on my book Causal Inference in Statistics, with Exercises, Practice Projects, and R Code Notebooks, for which Chapter 1 is available for free. The book provides a comprehensive coverage of causal inference weaving together both the potential outcomes frameworks and structural causal models, which are discussed below.
A Clash of Titans
Donald Rubin, a statistician who rediscovered the potential outcomes notation \((Y_i(1),Y_i(0))\) in 1974, sees the core task of causal inference as contrasting these potential outcomes. His differences with Pearl are stark:
“To avoid conditioning on some observed covariates [as Pearl suggests] in the hope of obtaining an unbiased estimator because of phantom but complementary imbalances on unobserved covariates, is neither Bayesian nor scientifically sound but rather it is distinctly frequentist and nonscientific ad hocery.”
Judea Pearl, a computer scientist who developed Structural Causal Models (SCMs), views the core task as estimating what happens to systems of variables when perturbed through intervention. He responds with equal conviction:
“Rubin will do well to expand the horizons of his students with some of the tools that his admirers now deem illuminating.”
The Potential Outcomes Framework
Rubin Causal Model
The Rubin Causal Model centers on a population of units, which we assume for simplicity is complete, so there are no sampling concerns. We label each unit \(i = 1,...,N\). Then, we define
- A set of covariates, \(X_i\)
- Two possible treatments, \(\mathbb{T} \in \{0,1\}\)
- The treatment actually taken by unit \(i\), denoted \(W_i\)
- Two potential outcomes, for each unit \(i\): \(Y_i(0)\) and \(Y_i(1)\)
The observed outcome is then given by: \[Y_i^{\text{obs}} = Y_i(1)\cdot W_i + Y_i(0)\cdot(1-W_i) = Y(W_i).\] While the unobserved (missing) outcome is:
\[Y_i^{\text{mis}} = Y_i(1)\cdot(1-W_i) + Y_i(0)\cdot W_i = Y(1-W_i).\]
The individual treatment effect is the contrast between these two potential outcomes, such as \[Y_i(1) - Y_i(0) \text{ or } Y_i(1)/Y_i(0).\]
The Treatment Assignment Mechanism
In Rubin’s framework, the central task of causal inference is modeling the treatment assignment mechanism - a probability distribution \(P(W|X, Y(0), Y(1))\) that can depend on both covariates and potential outcomes and models the probability of particular set of assignments of treament to units.
The Perfect Doctor: A Revealing Thought Experiment
To understand why treatment assignment mechanisms matter so deeply, consider the scenario of a “perfect doctor” who somehow knows - with absolute certainty - how each patient would respond to both treatment and control. This physician then assigns treatment only to those who will benefit.
Assuming we could see the true potential outcomes (which is impossible in reality), the treatment assignment might look like this:
| \(i\) | \(Y_i(0)\) | \(Y_i(1)\) | \(W_i\) | \(Y^{obs}\) | Individual Treatment Effect |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | -1 |
| 2 | 1 | 0 | 1 | 0 | -1 |
| 3 | 1 | 1 | 0 | 1 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | -1 |
| 6 | 1 | 1 | 0 | 1 | 0 |
In this example, lower values represent better outcomes (perhaps “0” means cured, while “1” means disease persists). The perfect doctor assigns treatment (\(W_i = 1\)) precisely to those patients (1, 2, and 5) who would benefit from it, while withholding treatment from those who wouldn’t benefit (3, 4, and 6).
If we calculate the true Average Treatment Effect using all potential outcomes: \[\text{ATE} = (-1 + -1 + 0 + 0 + -1 + 0) / 6 = -3/6 = -1/2.\] This tells us the treatment improves outcomes by 0.5 units on average across the entire population, of alternatively, it cures the condition for half the population. In this thought experiment, his is the true causal effect of treatment, because we know both potential outcomes for each unit.
However, in practice, we can only compare the observed outcomes between treated and control groups: \[\hat{\text{ATE}}_{\text{naive}} = \bar{y_1} - \bar{y_0} = \frac{(0 + 0 + 0)}{3} - \frac{(1 + 0 + 1)}{3} = 0 - 2/3 = -2/3\] This naive estimate suggests the treatment improves outcomes by 0.667 units - an overestimation of the true effect!
Why Perfect (Imperfect) Doctors Make Observational Studies Difficult
The critical insight is that this discrepancy isn’t random statistical noise - it’s a systematic bias resulting directly from how treatment was assigned. The doctor preferentially gave treatment to those who would benefit most, creating a treated group that’s fundamentally different from the control group in terms of their potential outcomes.
The doctor does not need to be perfect. Even imperfect doctors who systematically increase the probability of treatment for patients likely to benefit (as any good doctor would) will create this same pattern of bias. It is not difficult to imagine that outside of an experimental context, this sort of assignment to treatment conditions based on the results we expect from it is widespread. For example, people that have a higher probability of attending university might do so partially because they estimate that they will benefit more from it than those who have a lower probability of attending. This is of course desirable in everyday life: we make decisions based on the outcomes we expect from them. But this makes observational causal inference extremely challenging. Indeed, Rubin’s model shows that the probability of receiving a treatment, sorting into a group, or being exposed to a certain variable, must be independent of the outcome this variable entails if we wish to estimate the causal effect of the treatment on the outcome. This is precisely why randomization is so powerful - it breaks the dependency between treatment assignment and potential outcomes. As a matter of fact, in a randomized experiment, a random number is the only reason that a unit is given treatment or not, the treatment assignment is independent of everything by design (a random number is just random, and does not depend on anything else in the world). This allows us to estimate causal effects without bias, and Fisher was the first to strongly put forth this idea and change the face of experimental science forever.
In observational studies, where randomization isn’t possible, this bias drives our focus on balancing covariates that predict treatment assignment, essentially trying to approximate the independence that randomization would have provided. Here, randomization isn’t possible, so we try to approximate this independence by comparing patients with similar covariates, assuming that conditional on these covariates, treatment assignment is essentially random. Formally, \[P(W_i|X_i, Y_i(0), Y_i(1)) = P(W_i|X_i).\]
This is the key insight of the Rubin Causal Model: if treatment assignment is independent of potential outcomes given covariates, we can estimate unbiased treatment effects by comparing similarly situated treated and untreated units. This drives the focus on balancing covariates through matching, weighting, stratification, or regression. See the article by Andy Wilson and Aimee Harrison for a crash-course on applying these different techniques to remove confounding from causal estimate.
The Structural Causal Models Approach
Pearl’s framework uses Directed Acyclic Graphs (DAGs) and functional relationships to model causal systems. For example:
Where \(U\) variables represent independent error terms.
The causal effect of \(X\) on Y \(is\) defined as \(P(Y|do(X=x))\) - the distribution of \(Y\) under an intervention that sets \(X\) to \(x\). This do-operator is an invention of Pearl and distinguishes between mere observation and active intervention.
Intervention is modeled by severing all arrows entering X in the DAG, propagating this change through the system:
\[\begin{align*} X &\leftarrow s \\ Y &\leftarrow f_Y(s + S + U_Y) \\ S &\leftarrow f_S(U_S) \end{align*}\]In observational settings, we can’t directly observe the effect of intervention, so \[P(Y|X=x) \neq P(Y|do(X=x)).\] Pearl developed the backdoor criterion to find adjustment sets \(Z\) that satisfy: \[P(Y|do(X=x), Z) = P(Y|X=x, Z=z).\] This allows us to compute causal effects as a weighted average:
\[\begin{align*} P(Y|do(X=x)) &= \sum_{Z=z} P(Y|do(X=x), Z=z)P(Z=z) \\ &= \sum_{Z=z} P(Y|X=x, Z=z)P(Z=z), \end{align*}\]where the last equality holds because \(Z\) is assumed to satisfy the backdoor criterion, making \(P(Y|do(X=x), Z=z) = P(Y|X=x, Z=z)\). See the article by Andy Wilson and Aimee Harrison for a crash-course on applying the backdoor criterion to identify adjustment sets that remove confounding and allow estimation causal effects.
The M-Bias Controversy
The intellectual tension between these frameworks erupted into open controversy following a 2007 paper by Rubin. In The design versus the analysis of observational studies for causal effects, Rubin advocated controlling for any covariate measured before treatment assignment. Pearl-influenced scholars quickly identified this as problematic, based on their understanding of colliders and backdoor paths.
Confounders vs. Colliders–A Brief Review
In Pearl’s framework1, a confounder creates a
backdoor path between treatment and outcome. Adjusting for such
variables using the backdoor criterion allows identification of causal
effects.
A collider, by contrast, blocks a backdoor path between treatment and outcome. Adding such a variable to the adjustment set creates spurious associations.
If you want to learn more about colliders and confounders in Directed Acyclic Graphs, including numerical examples and how to identify them, you can check out my article on common DAG structures, and my article on selection bias, which explains how what statisticians have traditionally called selection bias can be modelled using colliders in DAG. This latter article also contains an R code notebook to practice your understanding with data.
Statisticians were already familiar with post-treatment adjustment bias (like differential loss to follow-up), but the M-bias scenario presented a new challenge.
The “Aha!” Moment: M-Bias
In 2008, Ian Shrier wrote a letter, which triggered a sequence of exchanges2, asking if Rubin had considered the following DAG structure:
In this DAG, \(Z_2\) is a pre-treatment variable, while \(Z_1\) and \(Z_3\) are unmeasured. Following Rubin’s advice, researchers would adjust for \(Z_2\), but the backdoor criterion reveals this would actually create collider bias that couldn’t be remedied because \(Z_1\) and \(Z_3\) are unmeasured. Pearl joined the debate, presenting this as refutation of Rubin’s blanket recommendation. Rubin eventually responded that the example was too contrived to be practically relevant. As Rubin tersely put it:
“Time spent designing observational studies to have observed covariate imbalances because of hoped-for compensating imbalances in unobserved covariates is neither practically nor theoretically justifiable.”
He further added:
“To avoid conditioning on some observed covariates in the hope of obtaining an unbiased estimator because of phantom but complementary imbalances on unobserved covariates, is neither Bayesian nor scientifically sound but rather it is distinctly frequentist and nonscientific ad hocery.”
The Real Meaning of M-Bias
The M-bias DAG encodes multiple conditional independencies:
\[\begin{align*} X &\perp Z_2 | Z_1\\ X &\perp Z_3\\ Z_1 &\perp Z_3\\ Z_1 &\perp Y | W\\ Z_2 &\perp Y | W, Z\\ Z_2 &\perp Y | Z_1, Z_3 \end{align*}\]Rubin’s argument essentially boils down to this: assuming this exact set of conditional independencies is not sufficient reason to refrain from adjusting for a pre-treatment variable. M-bias may be a theoretical curiosity but not a practical concern.
The debate has continued with increasingly pointed language. In a 2022 interview3, Pearl maintained:
“Rubin’s potential outcome framework became popular in several segments of the research community […]. These researchers talked ‘conditional ignorability’ to justify their methods, though they could not tell whether it was true or not. Conditional ignorability gave them a formal notation to state a license to use their favorite estimation procedure even though they could not defend the assumptions behind the license. […] It is hard to believe that something so simple as a graph could replace the opaque concept of ‘conditional ignorability’ that people find agonizing and incomprehensible. The back-door criterion made it possible.”
Yet it remains unclear how we can verify the truth of a DAG any more readily than we can verify conditional independencies between counterfactuals! They are both theoretical constructs that can’t be directly observed, but must be assumed based on our understanding of the system under study, plausibility of competing explanations, and many-other features of scientific research that are not easily formalized. The main contribution of the modern understanding of causal inference is precisely that we now know that any causal inference requires a leap of faith, as the assumptions needed can never be verified in the data. They can only be made more or less plausible by use of domain knowledge, theory, and other sources of information.
A Pragmatic Middle Ground
Both approaches have tremendous value, and the intellectual battle has driven progress in causal inference. Rather than choosing sides, practitioners can benefit from understanding both frameworks:
- DAGs are extremely useful for encoding complex conditional independencies, but they should be informed by thinking in terms of counterfactuals. Their apparent simplicity can be misleading in practice.
- Potential outcomes provide elegance without requiring new tools beyond counterfactual thinking, while SCMs require additional concepts like d-separation and the backdoor criterion.
In my opinion, causal inference is most clearly thought as a comparison of potential outcomes, but the DAG framework is an essential tool for understanding the structure of causal systems. The two approaches are complementary, not mutually exclusive. Richardson and Robins’ “Single World Intervention Graphs” (SWIGs) work attempts to formalize this unification, though the resulting framework is quite complex4.
Each approach has different strengths: SCMs may be more useful in tightly-controlled environments like online settings, while potential outcomes may be better for complex, less-controlled environments in social and health sciences where design aspects help eliminate competing explanations.
Most researchers care primarily about practical aspects of causal inference rather than philosophical underpinnings, similar to how working statisticians often blend Bayesian and frequentist approaches pragmatically.
Conclusion
The battle between Pearl and Rubin has produced tremendous insights and accelerated the development of causal inference methodologies. While philosophical differences remain, practitioners should feel free to use tools from both traditions as appropriate for their specific problems.
As I argue in my book Causal Inference in Statistics, with Exercises, Practice Projects, and R Code Notebooks the two frameworks are complementary. DAGs help with the problem of identification, while potential outcomes excel at addressing estimation, sampling, and design concerns. By understanding the strengths and limitations of each approach, researchers can develop more powerful and nuanced approaches to drawing valid causal conclusions from data.
Rather than choosing sides in this intellectual battle, our goal should be to advance science by using the best tools available for each specific problem.
More Resources
- If you are interested in Consulting, Training, Workshops, Public Speaking, Guest Lectures, and Other Custom Services in statistics and causal inference, please do not hesitate to contact me belairjustin@gmail.com
- The first chapter of my book, Causal Inference in Statistics, is available for free on my website by clicking here
- I share a montly newsletter to stats nerds, causal inference enthusiasts, and data scientists, subscribe here
- I am working online an online course, Introduction to Biostatistics
- I share statistics and causal inference content daily on Linkedin, where I’ve created a Linkedin Causal Inference Group
- Visit my personal website for more information on my work and to download the slides from this lecture.
References
Pearl, J. (2009). Causality: Models, Reasoning, and Inference (2nd ed.). Cambridge University Press.↩︎
- Rubin, D. B. (2007). The design versus the analysis of observational studies for causal effects: Parallels with the design of randomized trials. Statistics in Medicine, 26(1), 20–36.
- Shrier, I. (2008). Letter to the Editor. Statistics in Medicine, 27(14), 2740–2741. https://doi.org/10.1002/sim.3172 Rubin, D. B. (2008). Author’s reply. Statistics in Medicine, 27(14), 2741–2742. https://doi.org/10.1002/sim.3173
- Pearl, J. (2009). Remarks on the Method of Propensity Score (Letter to the Editor). Statistics in Medicine, 28(9), 1415–1416. https://doi.org/10.1002/sim.3531
- Sjölander, A. (2009). Propensity scores and M-structures. Statistics in Medicine, 28(11), 1416–1420. https://doi.org/10.1002/sim.3532
- Rubin, D. B. (2009). Should observational studies be designed to allow lack of balance in covariate distributions across treatment groups? Statistics in Medicine, 28(11), 1420–1423. https://doi.org/10.1002/sim.3565
Pearl, J. (2022). Causal Inference: History, Perspectives, Adventures, and Unification (An Interview with Judea Pearl). Observational Studies, 8(2), 7–94. https://doi.org/10.1353/obs.2022.0001↩︎
Richardson, T. S., & Robins, J. M. (2013). Single World Intervention Graphs (SWIGs): A Unification of the Counterfactual and Graphical Approaches to Causality (Working Paper No. 128). Center for Statistics and the Social Sciences, University of Washington.↩︎