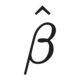Selection Bias, A Causal Inference Perspective (With Downloadable Code Notebook)

Example: College Admissions

Consider college admissions where students can be admitted based on either high intellectual ability or high athletic ability. Let’s simulate some data where these abilities are actually independent in the population. Next, we create an indicator for admission based on whether a student has high intellectual ability or high athletic ability. We then plot the data to see how the selection process affects the relationship between intellectual and athletic ability.

selection.bias <- data.frame("intellectual.ability" = rnorm(500, 0, 1),
                             "athletic.ability" = rnorm(500, 0, 1)
                             ) %>%
  mutate(admission = (intellectual.ability > 1) | (athletic.ability > 1.5)
         )

If you want to access the code to create the plot below, the code RMarkdown notebook used for this blog post is available for free on Github.

From this plot, we see that there is basically no relationship between intellectual and athletic ability in the population. Indeed, when fitting a linear regression model, we get a slightly negative slope.

lm(athletic.ability ~ intellectual.ability, data= selection.bias) %>%
  summary()

## 
## Call:
## lm(formula = athletic.ability ~ intellectual.ability, data = selection.bias)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.94113 -0.74507  0.01663  0.72882  3.11131 
## 
## Coefficients:
##                      Estimate Std. Error t value Pr(>|t|)
## (Intercept)          -0.04496    0.04730  -0.951    0.342
## intellectual.ability -0.04308    0.04678  -0.921    0.358
## 
## Residual standard error: 1.057 on 498 degrees of freedom
## Multiple R-squared:  0.0017, Adjusted R-squared:  -0.0003048 
## F-statistic: 0.848 on 1 and 498 DF,  p-value: 0.3576

Yet, the coefficient is not significantly different from 0. We know (because we generated the data) that the real-value is 0.

However, when we condition on admission, we see a strong negative relationship between intellectual and athletic ability.

This is confirmed by estimating the coefficient of the linear regression model when conditioning on admission.

lm(athletic.ability ~ intellectual.ability, data= selection.bias %>% filter(admission)) %>%
  summary()

## 
## Call:
## lm(formula = athletic.ability ~ intellectual.ability, data = selection.bias %>% 
##     filter(admission))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.1910 -0.6481  0.1565  0.8005  2.1926 
## 
## Coefficients:
##                      Estimate Std. Error t value Pr(>|t|)    
## (Intercept)            1.2034     0.1540   7.816 2.96e-12 ***
## intellectual.ability  -0.7471     0.1071  -6.974 2.14e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.143 on 114 degrees of freedom
## Multiple R-squared:  0.299,  Adjusted R-squared:  0.2929 
## F-statistic: 48.63 on 1 and 114 DF,  p-value: 2.142e-10

We obtain a highly significant negative coefficient. While this is visually intuitive in this specific example, it is not always so clear in real-world data. This is why it is important to learn to draw meaningful DAGs to represent background knowledge. In this specific example, it would look like this.

The theory of graphical causal models developed by Judea Pearl and others tells us that when there is a path between two variables of the form athletic_ability -> admission <- intellectual ability the variable admission is a collider. The concept of d-separation tells us that conditioning on a collider induces spurious correlation and biases the (causal) estimate we are seeking to establish¹.

It is not always obvious that our analysis is ‘conditional’ on a given variable when it is done through a selection mechanism. Oftentimes, we simply work with a dataset at hand and do not know immediately know the selection process that generated it. In this example, we implicitly condition on the admission variable if we simply select a sample from a university. I hope it is obvious that this form of bias can be lurking in many real-world problems, and it is one of the reasons why any experienced statistician always advises to study deeply the data-generating process.

By this, it is meant that before doing any sort of analysis, a deep investigation of the origin of the data is warranted. This means understanding how and why it was collected, who was responsible for collection, was there any processing done before sending it to the statistician, was there a data management protocol specified in advance, is there specific domain-knowledge that the statistician should know, etc. In many cases, data is handled by research assistants, is generated by software, or is collected by a third-party. In these cases, the statistician should be in open discussion with anybody responsible for the data and any domain expert that can help gain any insight into the data.