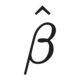Once Upon a Time Series

In the summer of 2015, I started to feel hope. Not that I was in a bad place—not at all.

In four months, I would go on to defend my doctoral dissertation in biostatistics at a top-notch school of public health. I’d originally intended to focus on causal inference under the keen guidance and mentorship of Professors Michael Hudgens and Amy Herring.

Causal inference covers two broad areas. In experimental studies, some variable X is randomized or otherwise manipulated or assigned. This isn’t true in observational studies. The goal of causal inference in both is to guess the effect (if any) of X on some other variable Y.

I would eventually focus on the observational side. And six years later, I would invent a way to conduct causal inference using non-experimental time series data. But how did all of this happen?

Potential Fear of Missing Outcomes

Michael had pioneered an area of causal inference called interference. Given his expertise, we initially explored how to extend principal stratification methods. But after a year, we realized we didn’t have enough real-world data to test our proposed approaches.

Fortunately, Amy was an expert in missing data and longitudinal analysis. As luck would have it, causal inference and missing data methods share common roots. So we pivoted my dissertation into how to handle longitudinal missing data—of which we had plenty!

Four years into my doctoral program, I’d finally found a path to graduation. But in May 2015, the causal inference FOMO was stronger than ever. That’s when Professor Susan Murphy came to campus.

Just-in-Time Advice and Inspiration

Susan specializes in personalized causal inference. During her two-part distinguished lecture series, she told us about building methods for finding good personalized treatment plans.

These plans are called adaptive treatment strategies or dynamic treatment regimes. They give each person a playbook of treatment decisions to make. With this type of plan, you can make ongoing treatment decisions based on your own progress.

Contrast this with interventions that are commonly tested in randomized controlled trials (RCTs). All participants in each RCT study arm follow a fairly rigid course of treatment.

But how good is a particular adaptive treatment plan? Susan and others answer this question by designing and running specialized RCTs designed to estimate the average effects of following such a plan.

At any point during the trial, a particular decision made by an average participant can have an average proximal effect given their own personal history of decisions and outcomes. By the end of the trial, these proximal effects can add up to an average overall distal effect of using that plan to make sequential treatment decisions.

Susan’s lectures captivated me. They were also extremely intimidating! The degree of technical art and skill she exercised in her work seemed way, way out of reach for an applied statistician like me. But then, maybe towards the end, she mentioned something called an “n-of-1 trial”.

“A Self that Goes on Changing”^[1]

An n-of-1 trial is a crossover RCT conducted on one person. (In finance, they’re called “switchback experiments”.) The type of treatment tested in an n-of-1 trial is more like that in an RCT: It doesn’t really change or adapt to past responses in an ongoing way as the trial progresses.

The complete relevant history of the person—a set of distinct time points relevant to the health condition being studied—is the “eligible target population” in an n-of-1 trial. For just that one person, the trial estimates a lifelong, stable, recurring individual treatment effect called the average period treatment effect (APTE).

The other trial designs Susan had described rely on population averages: How does this particular adaptive treatment plan compare to another plan (or standard of care) on average across an eligible target population of distinct people?

An n-of-1 trial instead considers each person to be an entire “population-of-one” (Daza, 2018). It answers the question of how good a particular treatment is for a particular person—not on average across people.

After Susan’s lectures, I wondered if this could be my Next Big Thing. Could I build a career around n-of-1 statistical methods?

Three factors locked it in:

1. A loved one of mine had irritable bowel syndrome (IBS), a chronic gastrointestinal illness with highly idiosyncratic triggers that varied in type and degree across people. IBS was a health condition that could really benefit from an n-of-1 approach!
2. Wearable sensors and self-tracking apps had been popping up everywhere. They generated an incredible amount of intensive longitudinal data—the fuel that drives time series analysis. And what were n-of-1 data if not multivariate time series?
3. An n-of-1 trial randomizes or otherwise assigns interventions. But real-world data from wearables and apps weren’t randomized or assigned—just like the observational data of groups and populations commonly analyzed in epidemiology. So I wasn’t surprised to find almost nothing in the scientific literature on how to conduct (observational) causal inference on n-of-1 data.

To this day, you won’t mistake me for a mathematical statistician. But even back then, I was comfortable teaching the foundations of causal inference. I knew I couldn’t do anything technical that would come anywhere close to what Susan and others could do.

But I had an idea: I could take existing observational causal inference methods and adapt them to real-world n-of-1 time series data from sensors and apps.

“It Needs Work”

During my three-year postdoc, I kept coming back to this idea. It started as a simple poster that showed how to apply textbook time series analysis to self-tracked health data, with some causal inference bells and whistles.

At a 2017 causal inference conference, I ran into an old college acquaintance of mine—who by then was a growing expert in the field. They took one look at my poster and remarked: “I like it. It needs work.”

I took their pithy advice and encouragement to heart. Over the next few years, I updated my ideas with more nuanced theory, shown in the poster below.

My postdoc mentor (and now good friend) Mike Baiocchi liked the way I was really “swinging for the fences” with this project. I told him that I really didn’t have a choice: I was nearing 40, and needed to jump-start my second career. The stakes were high!

Then I got my big break.

Fear the Decision Tree

The Quantified Self is “an international community of users and makers of self-tracking tools who share an interest in ‘self-knowledge through numbers.’” In 2017, they put together a special issue for a scientific journal on this theme. I submitted my poster’s corresponding manuscript.

In it, I laid out an analytical framework built around the APTE. I created this framework as a way for anyone to apply causal inference methods to n-of-1 data—both experimental and observational. To show that it was useful, I applied two common methods (g-computation and propensity score weighting) to my own weight and physical activity data.

After a number of largely cosmetic revisions, my manuscript was published in 2018 as “Causal Analysis of Self-tracked Time Series Data Using a Counterfactual Framework for N-of-1 Trials”. I was ecstatic! After a decade, I had finally arrived on the causal inference scene.

But this milestone was only the beginning. I’d just started figuring out how to replace time series models (which are linearized) with more flexible machine learning models like random forests. There was still so much to do, so I set my sights on university faculty positions.

Job applications for these roles require you to write a research plan. I eagerly sketched out my ideas, believing that faculty search committees would see the obvious value of my work. I just knew they would appreciate the ridiculously good timing of applying n-of-1 methods in this new age of personalized wellness and digital health.

I was wrong. At best, they probably saw my application and thought, “We like it. It needs work.”

“Outside Your Field”^[2]

By the time my postdoc ended in 2018, I’d failed to get an academic job. And I’d only written one n-of-1 paper; my “paper-of-1”. So I pivoted back to what I knew: industry. I joined a healthcare tech startup, far away from any work on n-of-1 studies and digital health data.

I was happy to find enjoyable work that stretched and expanded my skill set. There, I met one of my favorite lifelong colleagues. I got deep into the nitty-gritty of industry data science. And I would learn that biostatistics and health data science had a lot in common—but also how different they were.

I did manage to continue working on n-of-1’s outside of my full-time role. Early in 2019, I was surprised and delighted to be invited by Professor Jane Nikles and Dr. Suzanne McDonald to become a guest editor for a scientific journal’s n-of-1 special issue.

Jane and Suzanne are world-class experts in n-of-1 trial design and implementation. They founded the International Collaborative Network for N-of-1 Trials and Single-Case Designs (ICN), a “global network … interested in N-of-1 trials and single-case designs”. The ICN really helped kick-start my entry into the n-of-1 world.

But my day job took me further and further away from the n-of-1 world. I was still obsessed with the subject. How could I keep going? An unexpected path appeared the following year.

“Isa Lang, Marami Din”^[3]

I’d planned to attend a health behavior conference in April 2020, where I could promote my n-of-1 paper. Working in industry, I knew that branding was key to promoting products and services. And remember that n-of-1 research plan I’d written? Without university support, I needed to pursue it somewhere else.

That January, I also got an opportunity to share my professional journey as a scientist. Some of my Filipino colleagues had recommended me to Pinoy Scientists, an “online platform that gives a voice to brilliant scientists from the Philippines.” They assigned me to a one-week Instagram (IG) takeover, where I blogged about my scientific life.

That’s when it all clicked into place. I needed a brand and a space to pursue my research plan. And from my IG takeover, I knew I could write a blog. So in February 2020, I launched a newsletter about n-of-1 statistics. I called it Stats-of-1.

I was thrilled for this new, exciting, engaging way to continue my work. At Stats-of-1, we would build a community of n-of-1 methodologists—and in the process tell the world all about how incredibly useful these “esametric” designs could be.

And then, just a few weeks later, my entire team at work was laid off.

A Time Series of Fortunate Events

Excitement quickly crashed into job-loss anxiety. My priorities immediately shifted from getting the blog up and running to finding work. But just as suddenly as that door closed, another—a better—door opened.

I’d been keenly interested in a digital health startup called Evidation since I first learned about them during my postdoc. Their mission is “to create new ways to measure and improve health in everyday life.” We were both ridiculously aligned in both mission and approach.

Within a month of losing my job, Evidation posted an open role for a biostatistician—a statistically significant moment, to say the least! Three months hence, I would start my dream job.

I had no idea all this would happen. Or that, within a year, two amazing co-editors would join Stats-of-1—and that we would start a companion podcast two years later. At last, I could return to my singular fixation: n-of-1 causal inference.

Motoring Along

Late in 2020, my good colleague Professor Katarzyna “Kate” Wac introduced me to Igor Matias. Igor was a first-year computer science PhD student. He was eager to apply innovative approaches in healthcare, both broadly and specifically to screen people for Alzheimer’s Disease. Igor would become one of my closest colleagues.

Kate and I had previously designed, run, and written about an n-of-1 trial we’d conducted on ourselves (on the heterogeneous effects of sleep deprivation on blood glucose and mood). She and Igor were just starting to write their own paper. Kate wanted to take an n-of-1 approach, so she enlisted my help.

We examined variables like total sleep time (TST), socializing, exercise, and stress—and their relationships to heart rate. I wanted us to be able to talk about tenable causes and effects, not just correlations. But none of our variables had been randomized.

So as 2021 was just beginning, I used my APTE framework to create a causal inference method called MoTR (pronounced “motor”). The three of us used MoTR to discover and statistically test plausible effects. A year and a half later, we published our paper as “What possibly affects nighttime heart rate? Conclusions from N-of-1 observational data.”

But why did we even need MoTR—and how exactly does it work?

A Head of My Self^[4]

Say I keep a daily migraine diary. I record how many migraines I get on a given day. I also record possible triggers, like how much coffee I drink on a given day. I want to know if drinking coffee affects my migraines.

In my data, I notice that I tended to suffer a migraine attack whenever I drank more coffee. I convince myself that it’s worth testing this hypothesis. Soon, I begin to self-experiment with my coffee consumption.

I endure my self-imposed n-of-1 trial for two months, but am ultimately disappointed. Randomizing how much coffee I drank each day didn’t meaningfully change the probability of suffering a migraine attack. What happened?

What I didn’t know was that drinking more coffee did not in fact increase my migraine chances. I also didn’t know that getting a migraine the day before caused me to sleep less—and this tended to make me drink more coffee the next day (outside of my n-of-1 trial). A migraine attack yesterday also directly increased my chances of getting a migraine today.

And in my particular case, something else was true. Whenever I had a migraine attack the day before, this somehow activated coffee enough to induce a migraine attack the next day. In statistics, we call this an interaction. In causal inference, we call migraine an effect modifier: It modified (here, activated) the effect of coffee consumption on my migraines the next day.

Together, these personal health facts led to the spurious correlation I’d found—that then became my mistaken hypothesis. Could I somehow have avoided going through all this, only to find I was wrong?

By March 2021, the answer was a qualified yes. I would simply need to replicate myself.

To A/B, or Not to A/B

Let’s review how observational causal inference works.

Say you have some real-world data. You’re interested in how changing variable X may have caused variable Y to change (on average). Your problem: X was never systematically randomized or experimentally manipulated.

You try fitting a bunch of models to describe Y as a function of X. But you know these models can only ever help you guess the correlation (statistical association) between X and Y. You know that it’s impossible for any model alone—artificial intelligence (AI) included—to help you reliably guess the average effect of X on Y.

Thankfully, there is a narrow path forward. All you have to do is correctly guess most of the strongest factors that can affect both X and Y. Then you also have to correctly guess some of the ways these factors relate to X, Y, and each other.

These “ways” are called causal assumptions, mechanisms, or models. A guess is correct if it sufficiently represents the true nature of reality.

In the statistics approach to epistemology (the building of knowledge), randomizing X ideally eliminates the need for this guessing. This is why we statisticians like it! Without randomization, we know there is no free lunch to test if and how X affects Y (on average).

ATE Expectations

In your non-randomized observational study, guesses are all you’ve got. You’re comforted that some of these causal factors and assumptions may already have been established as scientific facts. They will help you decide how Y might change if you change each of the causal factors—at least some of which are causes (X included).

But you’re really most interested in the average treatment effect (ATE) of changing X on Y. The ATE is the real, true effect of X on Y averaged over all other causal factors, however the latter may vary in the “real world”.

The ATE is the exact quantity that randomizing X would have allowed you to estimate. And knowing how Y would have varied (its distribution) had X been randomized would have given you both faith (accuracy) and confidence (precision) in your estimate of that real, true quantity.

In your observational study, causal inference is the process of using causal assumptions (some assumed, some known) to mimic the distribution of Y had X been randomized. You are simply trying to mimic the results of an RCT to test the average effect of X on Y.

Whatever the Outcome

One way to mimic RCT results is through g-computation or the g-formula (a.k.a. standardization, back-door adjustment formula, regression adjustment).

This approach is super intuitive because in step one, you start by doing what you’ve always been doing: you model Y as a function of other variables. Here, the model explicitly represents how outcome Y might change if you change each of the causal factors included in the set of all predictors—including X, your main cause of interest.

In step two of g-computation, you predict Y for each study participant using the outcome model you’d fit to your observational data. This step assumes you can predict any participant’s Y value without needing to know the values of any other participant’s variables (including Y). That is, it assumes all participants are mutually independent.

But the brilliance of g-computation is in step three. You re-weight your predictions so that they vary amongst your participants in the same way as if X had been randomized—as if you’d run an RCT!

Actionable Twinsight

Now suppose Y, X, and all other predictors are time series variables. Instead of participants, we have time points or periods. The current period’s Y value may depend on past periods’ Y values. That is, Y could be autocorrelated—a very realistic possibility with n-of-1 data.

In Daza (2018), I’d defined the g-formula for partitioned time series data. But could I use the full g-computation process to mimic the results of an n-of-1 trial? Autocorrelation blocked step two from being done the usual way. And I’d also have to figure out how to re-weight each prediction in step three.

I was in a probability pickle. So what does a mathematically challenged statistician like me do? I simulate!

A simulation study is basically a home-brewed big data version of hand-wavy proof by induction. First, set or fix all of your parameters, models, and assumptions. Then generate a ton of systematically varying datasets with many known properties. Finally, take all of your synthetic data, shake off the extra bits, and collect the kernels of mathy insights that pop out.

So simulations were plenty on my mind when I first heard about “digital twins”.

Multitudinal^[5]

At Evidation, we were constantly awash in the intensive longitudinal data produced by each person’s wearable sensors and app-delivered survey responses. These were the same data types and structures Kate, Igor, and I had wrestled with in our paper.

It was in this data-intensive milieu that I really started paying attention to an interesting new-ish analytical approach. According to the Digital Twin Consortium, a digital twin is “a virtual representation of real-world entities and processes, synchronized at a specified frequency and fidelity.”

From their sub-definition: “Digital twins use real-time and historical data to represent the past and present and simulate predicted futures” (emphases mine). That was the spark!

I would simulate predicted pasts—replicate myself—as if I’d run an n-of-1 trial.

Current Time in Monte Carlo

Remember my disappointing migraine self-experiment?

Suppose I’d paid attention to whether or not I’d had a preceding migraine attack one day earlier. And suppose I’d had a good idea of how having or not having a migraine yesterday might have affected the chances of a migraine attack today—along with my suspected trigger, coffee.

In other words, suppose I had the right causal model (but not its parameters). This model can take any form—not just linearized—as long as it’s a proper prediction or classification function.

I could have used this model to sequentially predict my migraine chances after having suffered a migraine (or not) the day before, or after drinking a particular amount of coffee that day. In essence, this model would have been my digital twin—my “model twin”.

So how could I have used this model twin to estimate the true effect of coffee? Simple: by running it through a simulated n-of-1 trial! I therefore called this procedure “model-twin randomization” or MoTR.

Model Twin Study

Step one of MoTR is the same as in g-computation: fit the outcome model. But in step two, MoTR randomizes coffee consumption (X). And in step three, it sequentially predicts a migraine attack (Y). Like g-computation, this procedure mimics the distribution of migraine attacks (Y) had coffee consumption (X) been randomized.

I would then calculate the average outcome—the proportion of simulated migraine attacks over all study days—per treatment condition (X=1 for at least one cup of coffee that day, and X=0 otherwise). Finally, I’d calculate my estimated effect by contrasting these proportions in a sensible way; for example, as a risk difference: the probability of a migraine under X=1 versus that under X=0.

I’d have found that my risk difference is close to zero. (The small interaction I mentioned earlier would’ve made it a little greater than zero.) That is, I would’ve concluded that changing my coffee habits likely wouldn’t do much to prevent my migraines. I could have avoided my painful two-month-long n-of-1 trial.

That’s how “running the MoTR” helps you find only the most important, impactful triggers and causes. I explained it succinctly in 2021: “MoTR is fueled by a prediction model fit to real-world data and refined with explicit causal assumptions in order to generate actual effect estimates.”

It’s About Time

In the three years since, I’ve taken MoTR on the road.

Guest lectures at Brown, Harvard, Hopkins, Stanford, the University of the Philippines, the University of Minnesota, and the University of South Carolina. A series of n-of-1 sessions at the Joint Statistical Meetings (JSM), the annual flagship conference of the American Statistical Association. Same goes for the American Causal Inference Conference, and also the Society of Behavioral Medicine’s annual conference.

Lately, it’s been feeling like n-of-1’s are finally about to hit it big. Really big.

In 2022, both Forbes and Fortune magazine recognized Stats-of-1 for our innovative ideas about health and healthcare. MoTR is patent-pending as of 2023. And Fortune’s former Editor-in-Chief told me he believed in the potential of n-of-1 trials to reshape clinical studies.

Going it alone, big swings are all I’ve got. But I’ve tried to heed the wise words of Professor Patrick Onghena, a statistical giant in the field of single-case designs (cousins to n-of-1’s): “Even if one is a single-case researcher, it shouldn’t imply that one is a lonely researcher.”

I created Stats-of-1 to help us go far—together. It’s about time.