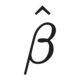How to Handle Influential Observations Using R (With Downloadable R Code Notebook)

Justin Bélair

Biostatistician in Science & Tech | Educator | Consultant | Causal Inference Enthusiast

By Justin Bélair © | Biostatistician at JB Statistical Consulting

Find the RMarkdown Notebook on Github and Run the Code Yourself!

Influential Observations vs. Outliers

Much has been said about handling outliers and influential observations, but what exactly do these terms mean and how can we go about dealing with such issues in a pragmatic way?

We’ll start by simulating data that follows a simple linear model + noise and in turn add observations that deviate from the model in different ways to determine the impact of such deviations on our statistical estimates.

An Influential Observation

set.seed(1) # for reproducibility

n <- 39 #number of observations

true.slope.coefficient <- 1

x <- rnorm(n, 1, 1) # x values

y <- true.slope.coefficient*x + rnorm(n, 0, 1) # y = x + epsilon

data <- data.frame(x = x, y = y) # data generated according to the model

influential <- c(6,3) # a value that doesn't follow the general pattern

data.influential <- rbind(data, influential) # we sneak the influential observation in the data

data.influential %>%
  ggplot(aes(x = x, y = y)) +
  geom_point() +
  geom_smooth(method="lm", se = FALSE) +
  geom_smooth(aes(x=x, y=y), data, method = "lm", se = FALSE, color = "red")

## `geom_smooth()` using formula = 'y ~ x'
## `geom_smooth()` using formula = 'y ~ x'

Here, the red line is the “true” unbiased OLS regression slope, whereas the blue line is influenced by the data point we added that doesn’t follow the main data pattern.

Residuals

Typically, visual checks of model residuals would help in finding outliers.

lm.influential <- lm(y ~ x, data=data.influential)

lm.influential.fitted <- predict(lm.influential)
lm.influential.residuals <- residuals(lm.influential)

residuals.influential.df <- data.frame(fitted = lm.influential.fitted, residuals = lm.influential.residuals) 

# We look at residuals vs fitted 

residuals.influential.df %>%
  ggplot(aes(x=fitted, y = residuals)) +
  geom_point()

# We look at QQ plot of residuals against standard gaussian

residuals.influential.df %>%
  ggplot(aes(sample = residuals)) +
  geom_abline(intercept = 0, slope = 1) +
  stat_qq()

Here, the typical visual diagnostics do not reveal any issues with residuals, if only that one data point does follow the pattern of fitted values of the data cloud - this is our first clue that something has gone awry!

Using `stats::influence.measures` in `R`

It is apparent from the plot of the blue regression line superimposed on the data cloud that the value at \(x=6\) does not conform to the pattern predicted by the main group of data points. In turn, the departure is so egregious as to completely undermine the validity of the estimated linear trend.

Let’s first compute the linear model without the influential data point and look at its residuals’ diagnostics plots.

lm.wo.influential<- lm(y ~ x, data=data)

lm.wo.influential.fitted <- predict(lm.wo.influential)
lm.wo.influential.residuals <- residuals(lm.wo.influential)

residuals.wo.influential.df <- data.frame(fitted = lm.wo.influential.fitted, residuals = lm.wo.influential.residuals) 

# We look at residuals vs fitted 

residuals.wo.influential.df %>%
  ggplot(aes(x=fitted, y = residuals)) +
  geom_point()

# We look at QQ plot of residuals against standard gaussian

residuals.wo.influential.df %>%
  ggplot(aes(sample = residuals)) +
  geom_abline(intercept = 0, slope = 1) +
  stat_qq()

There is nothing notable on the regression diagnostics.

To properly see the difference made by removing the influential observation, we can look more closely at the model coefficients with and without the influential observation.

coefficients(lm.influential)

## (Intercept)           x 
##   0.2557782   0.8509512

coefficients(lm.wo.influential)

## (Intercept)           x 
## -0.09762309  1.23608854

Indeed, looking at the model outputs with and without the so-called influential observation, we see that the estimated model coefficients are discrepant. These sorts of changes in model estimates attributable to one single data point can be measured using different influence measures. The default stats::influence.measures in R computes a handful of such useful measures.

Difference in Betas and Difference in Fits

The change in a fitted model parameter when we remove a data point from the dataset is referred to as DFBETA. For each beta coefficient of a given model, the DFBETA associated with data point \(i\) is simply

\[\text{DFBETA}_i = \hat{\beta} - \hat{\beta}_{(-i)},\]

where \(\hat{\beta}\) is the standard estimated coefficient and \(\hat{\beta}_{(-i)}\) is the coefficient estimated from exactly the same model, except the \(i\) data point is removed. For a model with \(p\) fitted parameters to \(n\) data points there is thus \(n\times p\) DFBETA measures available.

The influence.measures function returns a list with 2 important elements :

infmat contains a matrix of various influence measures computed on every single data point, including the DFBETAs of the previous section.
is.inf contains a matrix of logical values determining if, according to a given measure, a data point is deemed influential. Obviously, the cutoff at which a point is deemed influential according to a given measure is somewhat arbitrary.

Let’s take a look on our data.

# Without the influential
influence.measures.wo.influential <- influence.measures(lm.wo.influential)

influence.measures.wo.influential$is.inf

##    dfb.1_ dfb.x dffit cov.r cook.d   hat
## 1   FALSE FALSE FALSE FALSE  FALSE FALSE
## 2   FALSE FALSE FALSE FALSE  FALSE FALSE
## 3   FALSE FALSE FALSE FALSE  FALSE FALSE
## 4   FALSE FALSE FALSE  TRUE  FALSE FALSE
## 5   FALSE FALSE FALSE FALSE  FALSE FALSE
## 6   FALSE FALSE FALSE FALSE  FALSE FALSE
## 7   FALSE FALSE FALSE FALSE  FALSE FALSE
## 8   FALSE FALSE FALSE FALSE  FALSE FALSE
## 9   FALSE FALSE FALSE FALSE  FALSE FALSE
## 10  FALSE FALSE FALSE FALSE  FALSE FALSE
## 11  FALSE FALSE FALSE FALSE  FALSE FALSE
## 12  FALSE FALSE FALSE FALSE  FALSE FALSE
## 13  FALSE FALSE FALSE FALSE  FALSE FALSE
## 14  FALSE FALSE FALSE  TRUE  FALSE  TRUE
## 15  FALSE FALSE FALSE FALSE  FALSE FALSE
## 16  FALSE FALSE FALSE FALSE  FALSE FALSE
## 17  FALSE FALSE FALSE FALSE  FALSE FALSE
## 18  FALSE FALSE FALSE FALSE  FALSE FALSE
## 19  FALSE FALSE FALSE FALSE  FALSE FALSE
## 20  FALSE FALSE FALSE FALSE  FALSE FALSE
## 21  FALSE FALSE FALSE FALSE  FALSE FALSE
## 22  FALSE FALSE FALSE  TRUE  FALSE FALSE
## 23  FALSE FALSE FALSE FALSE  FALSE FALSE
## 24  FALSE FALSE FALSE  TRUE  FALSE  TRUE
## 25  FALSE FALSE FALSE FALSE  FALSE FALSE
## 26  FALSE FALSE FALSE FALSE  FALSE FALSE
## 27  FALSE FALSE FALSE FALSE  FALSE FALSE
## 28  FALSE FALSE FALSE FALSE  FALSE FALSE
## 29  FALSE FALSE FALSE FALSE  FALSE FALSE
## 30  FALSE FALSE FALSE FALSE  FALSE FALSE
## 31  FALSE FALSE FALSE FALSE  FALSE FALSE
## 32  FALSE FALSE FALSE FALSE  FALSE FALSE
## 33  FALSE FALSE FALSE FALSE  FALSE FALSE
## 34  FALSE FALSE FALSE FALSE  FALSE FALSE
## 35  FALSE FALSE FALSE FALSE  FALSE FALSE
## 36  FALSE FALSE FALSE FALSE  FALSE FALSE
## 37  FALSE FALSE FALSE FALSE  FALSE FALSE
## 38  FALSE FALSE FALSE FALSE  FALSE FALSE
## 39  FALSE FALSE FALSE FALSE  FALSE FALSE

We see that in the data without the influential observation, most measures consider the data points to not be influential, as expected. There are a few TRUE values in the matrix, which shows that even with data that perfectly agree with the assumptions needed for OLS regression, the influence measures are not perfect - this is a case of false positives.

# With the influential observation
influence.measures.influential <- influence.measures(lm.influential)

influence.measures.influential$is.inf

##    dfb.1_ dfb.x dffit cov.r cook.d   hat
## 1   FALSE FALSE FALSE FALSE  FALSE FALSE
## 2   FALSE FALSE FALSE FALSE  FALSE FALSE
## 3   FALSE FALSE FALSE FALSE  FALSE FALSE
## 4   FALSE FALSE FALSE FALSE  FALSE FALSE
## 5   FALSE FALSE FALSE FALSE  FALSE FALSE
## 6   FALSE FALSE FALSE FALSE  FALSE FALSE
## 7   FALSE FALSE FALSE FALSE  FALSE FALSE
## 8   FALSE FALSE FALSE FALSE  FALSE FALSE
## 9   FALSE FALSE FALSE FALSE  FALSE FALSE
## 10  FALSE FALSE FALSE FALSE  FALSE FALSE
## 11  FALSE FALSE FALSE FALSE  FALSE FALSE
## 12  FALSE FALSE FALSE FALSE  FALSE FALSE
## 13  FALSE FALSE FALSE FALSE  FALSE FALSE
## 14  FALSE FALSE FALSE  TRUE  FALSE FALSE
## 15  FALSE FALSE FALSE FALSE  FALSE FALSE
## 16  FALSE FALSE FALSE FALSE  FALSE FALSE
## 17  FALSE FALSE FALSE FALSE  FALSE FALSE
## 18  FALSE FALSE FALSE FALSE  FALSE FALSE
## 19  FALSE FALSE FALSE FALSE  FALSE FALSE
## 20  FALSE FALSE FALSE FALSE  FALSE FALSE
## 21  FALSE FALSE FALSE FALSE  FALSE FALSE
## 22  FALSE FALSE FALSE  TRUE  FALSE FALSE
## 23  FALSE FALSE FALSE FALSE  FALSE FALSE
## 24  FALSE FALSE FALSE  TRUE  FALSE FALSE
## 25  FALSE FALSE FALSE FALSE  FALSE FALSE
## 26  FALSE FALSE FALSE FALSE  FALSE FALSE
## 27  FALSE FALSE FALSE FALSE  FALSE FALSE
## 28  FALSE FALSE FALSE FALSE  FALSE FALSE
## 29  FALSE FALSE FALSE FALSE  FALSE FALSE
## 30  FALSE FALSE FALSE FALSE  FALSE FALSE
## 31  FALSE FALSE FALSE  TRUE  FALSE FALSE
## 32  FALSE FALSE FALSE FALSE  FALSE FALSE
## 33  FALSE FALSE FALSE FALSE  FALSE FALSE
## 34  FALSE FALSE FALSE FALSE  FALSE FALSE
## 35  FALSE FALSE FALSE FALSE  FALSE FALSE
## 36  FALSE FALSE FALSE FALSE  FALSE FALSE
## 37  FALSE FALSE FALSE FALSE  FALSE FALSE
## 38  FALSE FALSE FALSE FALSE  FALSE FALSE
## 39  FALSE FALSE FALSE FALSE  FALSE FALSE
## 40   TRUE  TRUE  TRUE FALSE   TRUE  TRUE

Here, we see that the last data point is flagged by multiple measures as being influential - which agrees with what we saw by looking at the plot. Indeed, when comparing the blue regression line with the red regression line above, we already had an idea that the estimated model was highly sensitive to the influential data point and that the red regression line seemed to lie closer to the data - here, we know this is the right model since we simulated the data from it.

DFFITS

Going back to our influence measure matrix, we notice that the data point is also considered influential according to the DFFITS measure, which is simply a Studentized measure of the difference between model predictions with and without the data point.

\[\text{DFFITS}_i = \frac{\hat{y}_i - \hat{y}_{(-i)}}{s},\]

where \(s\) is an appropriate Studentization term which we will discuss in an ulterior advanced article. Indeed, looking at the regression lines above with and without the influential data point clearly shows that the predicted \(y\) value at \(x=6\) is highly sensitive to the inclusion of the influential data point in the model fit :

\[ \hat{y}_{40} = \hat{\beta}_0 + \hat{\beta}_1 \times 6 = 0.256 + 0.851 \times 6 = 5.361 \]

\[ \hat{y}_{(-40)} = \hat{\beta}_{0(-40)} + \hat{\beta}_{1(-40)} \times 6 = -0.098 + 1.236 \times 6 = 7.319 \]

\[ \hat{y}_{40} - \hat{y}_{(-40)} = -1.957 \]

This value would then be Studentized to determine if it is large according to a given measure of standard deviation (again, we will get back to this in an ulterior advanced article).

An Outlier

outlier <- c(1,5) # a value that doesn't follow the general pattern

data.outlier <- rbind(data, outlier) # we sneak the outlier in the data

data.outlier %>%
  ggplot(aes(x = x, y = y)) +
  geom_point() +
  geom_smooth(method="lm", se = FALSE) +
  geom_smooth(aes(x=x, y=y), data, method = "lm", se = FALSE, color = "red")

## `geom_smooth()` using formula = 'y ~ x'
## `geom_smooth()` using formula = 'y ~ x'

We see from this plot that there is a data point located at \((1,5)\) that does not conform to the pattern in the data cloud, but removing barely alters the regression line (in red) - this point is thus not very influential. Below, a call to influence.measures confirms this!

lm.outlier <- lm(y ~ x, data=data.outlier)

influence.measures.outlier <- influence.measures(lm.outlier)

influence.measures.outlier$is.inf

##    dfb.1_ dfb.x dffit cov.r cook.d   hat
## 1   FALSE FALSE FALSE FALSE  FALSE FALSE
## 2   FALSE FALSE FALSE FALSE  FALSE FALSE
## 3   FALSE FALSE FALSE FALSE  FALSE FALSE
## 4   FALSE FALSE FALSE  TRUE  FALSE FALSE
## 5   FALSE FALSE FALSE FALSE  FALSE FALSE
## 6   FALSE FALSE FALSE FALSE  FALSE FALSE
## 7   FALSE FALSE FALSE FALSE  FALSE FALSE
## 8   FALSE FALSE FALSE FALSE  FALSE FALSE
## 9   FALSE FALSE FALSE FALSE  FALSE FALSE
## 10  FALSE FALSE FALSE FALSE  FALSE FALSE
## 11  FALSE FALSE FALSE  TRUE  FALSE FALSE
## 12  FALSE FALSE FALSE FALSE  FALSE FALSE
## 13  FALSE FALSE FALSE FALSE  FALSE FALSE
## 14  FALSE FALSE FALSE  TRUE  FALSE  TRUE
## 15  FALSE FALSE FALSE FALSE  FALSE FALSE
## 16  FALSE FALSE FALSE FALSE  FALSE FALSE
## 17  FALSE FALSE FALSE FALSE  FALSE FALSE
## 18  FALSE FALSE FALSE FALSE  FALSE FALSE
## 19  FALSE FALSE FALSE FALSE  FALSE FALSE
## 20  FALSE FALSE FALSE FALSE  FALSE FALSE
## 21  FALSE FALSE FALSE FALSE  FALSE FALSE
## 22  FALSE FALSE FALSE FALSE  FALSE FALSE
## 23  FALSE FALSE FALSE FALSE  FALSE FALSE
## 24  FALSE FALSE FALSE  TRUE  FALSE  TRUE
## 25  FALSE FALSE FALSE FALSE  FALSE FALSE
## 26  FALSE FALSE FALSE FALSE  FALSE FALSE
## 27  FALSE FALSE FALSE FALSE  FALSE FALSE
## 28  FALSE FALSE FALSE FALSE  FALSE FALSE
## 29  FALSE FALSE FALSE FALSE  FALSE FALSE
## 30  FALSE FALSE FALSE FALSE  FALSE FALSE
## 31  FALSE FALSE FALSE FALSE  FALSE FALSE
## 32  FALSE FALSE FALSE FALSE  FALSE FALSE
## 33  FALSE FALSE FALSE FALSE  FALSE FALSE
## 34  FALSE FALSE FALSE FALSE  FALSE FALSE
## 35  FALSE FALSE FALSE FALSE  FALSE FALSE
## 36  FALSE FALSE FALSE FALSE  FALSE FALSE
## 37  FALSE FALSE FALSE FALSE  FALSE FALSE
## 38  FALSE FALSE FALSE FALSE  FALSE FALSE
## 39  FALSE FALSE FALSE FALSE  FALSE FALSE
## 40  FALSE FALSE FALSE  TRUE  FALSE FALSE

Indeed, the outlier (observation number 40) does not seem particularly influential when compared with other data points, say observations 14 and 24.

Yet, we clearly see that this point has a problematic residual from the following diagnostics.

lm.outlier.fitted <- predict(lm.outlier)
lm.outlier.residuals <- residuals(lm.outlier)

residuals.df <- data.frame(fitted = lm.outlier.fitted, residuals = lm.outlier.residuals) 

# We look at residuals vs fitted 

residuals.df %>%
  ggplot(aes(x=fitted, y = residuals)) +
  geom_point()

# We look at QQ plot of residuals against standard gaussian

residuals.df %>%
  ggplot(aes(sample = residuals)) +
  geom_abline(intercept = 0, slope = 1) +
  stat_qq()

This point would typically be flagged as an outlier and further study might indicate a proper way of handling it - we never automatically remove it!

Takeaways

An influential observation is one that, when removed, significantly alters the model under investigation. It is discovered by using influence measures, although there is a subjective element in choosing a proper threshold for these measures.
An outlier is a data point that significantly departs from the pattern represented by the model under investigation. It is discovered using model residuals, although there is a subjective element in deciding when a residual is considered too large.
These two caracteristics need not coincide! Indeed, an outlier can be influential or not, and an influential observation can be an outlier or not.

References

This article was partly inspired by a great post on influential observations available at https://online.stat.psu.edu/stat462/node/170/.

How to Handle Influential Observations Using R (With Downloadable R Code Notebook)

Justin Bélair

Table of Contents

How to Handle Influential Observations Using R

Influential Observations vs. Outliers

An Influential Observation

Residuals

Using `stats::influence.measures` in `R`

Difference in Betas and Difference in Fits

DFFITS

An Outlier

Takeaways

References

Recent Posts

Biostatistics Consulting: A Comprehensive Guide

Simulating The Distribution of P-Values (With Downloadable R Code Notebook)

Tell Me About Yourself

What Are P-values And Why Are They So Problematic?

Tags

EXPLORE

How to Handle Influential Observations Using R (With Downloadable R Code Notebook)

Justin Bélair

Table of Contents

How to Handle Influential Observations Using R

Influential Observations vs. Outliers

An Influential Observation

Residuals

Using stats::influence.measures in R

Difference in Betas and Difference in Fits

DFFITS

An Outlier

Takeaways

References

Recent Posts

Biostatistics Consulting: A Comprehensive Guide

Simulating The Distribution of P-Values (With Downloadable R Code Notebook)

Tell Me About Yourself

What Are P-values And Why Are They So Problematic?

Tags

EXPLORE

Using `stats::influence.measures` in `R`