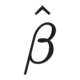Who’s the Culprit for Bias in Aging Clocks?

Predicting biological age with machine learning

How and why do we age?

This is a lofty biological question, so what might it have to do with machine learning and statistics? ML and statistics can play a pretty useful role in predicting the risk of someone developing an age-related condition later in life and disease progression. However, estimating one’s ‘biological age’ takes it a step further by systematically measuring biomarkers associated with aging to enable better prediction of one’s state of health and disease risk. Unlike chronological age which is directly measurable, biological aging is a latent concept that can inferred through various biological measures.

We make two assumptions when we develop and deploy age predictive algorithms to estimate aging:

1. Our bodies don’t age uniformly
2. Chronology is not the only way to understand the aging process.

In cognitive neuroscience, we call these ML algorithms “brain age models,” but brain scan-based models are not the only ones out there. I remember in my second year of graduate school, I told my bioinformatician friend about my project, and he said, “So you’re developing a brain aging clock!” I responded, “What do you mean by clock?” Eventually, I caught up with the literature in the broader field of computational biology and realized there are other algorithms based on epigenetic data and/or blood-based proteomic data. These ML algorithms are commonly referred to as “aging clocks.” We were simply using different field-specific terms for the same ML-based approach.

The earliest brain age models (Franke et al., 2010) and epigenetic aging (eAge) clocks (Hannum et al., 2013; Horvath et al., 2013) have been around for over 10 years now. I will refer to clocks and models interchangeably in the rest of the article.

Estimation bias in age prediction models

One of the key issues with brain age models is the consistent overestimation of age among younger adults and underestimation of older adults (typically > 60). When I first learned about the other types of aging clocks I wanted to find out if there were similar issues with these clocks. A commentary by Lange and Cole (2020) discussed four plausible explanations of the consistent over- and under-estimation of young and older adults that have been proposed by other researchers. In cognitive neuroscience, inconsistency of the noise distribution across the lifespan renders it particularly challenging for researchers to interpret the clinical validity of the prediction, especially during childhood and adolscence, especially since there is a lack of consensus on how to effectively model the non-linear and heterogeneous nature of developmental trajectories.

Inconsistency of Noise Distribution/Variability Across the Lifespan

Bias could be due to varying levels of noise in the data at different ages, which could affect the accuracy of age predictions (Cole et al., 2017). There just might be greater variation in brain structure among older healthy adults who have similar cognitive performance, than younger adults who also exhibit similar cognitive performance for their age group. This issue can be corrected by using a normative model in which various patterns of brain aging at different life stages is represented. By establishing a range of what “normal” looks like for different age groups, these models can better identify when noise or inconsistencies are influencing predictions. Additionally, when applying Hovarth’s eAge clock to data from adolescents, a log-transformation was needed to account for the non-linearities in aging during adolescence.

Sample Size Imbalance Across Age Groups

According to this explanation, the bias could be due to unequal sample sizes of different age groups used in training the models (Aycheh et al., 2018). For example, if there are more samples from younger or older age groups, it might skew the model’s predictions. It is challenging to collect data from older adults given that participants with limted mobility by default will be underrepresented in these studies – participants who end up enrolling and completing the study are typically healthy enough to do so. Hence we end up with a self-selected/biased sample.

“Quirky” Characteristics of the sample data

This account attributes the bias to the nature of the data used to train the models. When models are trained on heterogeneous data, they may capture site-specific or cohort-specific patterns rather than true age-related changes (Pardoe & Kuzniecky, 2018).

Regression to the mean

In the context of brain age prediction, for younger subjects, if the initial model predictions are not perfectly accurate and have some error, these predictions will likely be higher (closer to the mean age) than the true age. The opposite is true for older adults. While the other explanations above are plausible, this observed bias (overestimation for younger individuals and vice versa for older individuals) is remarkably consistent across different studies, datasets, and methods. This suggest a statistical explanation like RTM. Liang et. al. 2019 found that that various commonly applied methods for age prediction (ridge regression, support vector regression, Gaussian processes, deep neural networks) all exhibited similar biases.

Regression to the mean comes out as the top explanation, but I wondered if there were other biological explanations for this estimation bias, and if the same phenomena existed in aging clocks trained on epigenetic data. As it turns out, from the literature on eAge clocks, I found a few more potential explanations:

Survival bias of centenarians

Centenarians often have a predicted eAge younger than their true age has been interpreted as a sign of survival bias, where those with a lower biological age are more likely to live longer. However, if the clock systematically underpredicts age in older individuals, this interpretation might need reexamination. The younger predicted age might not necessarily reflect better health status but rather the model’s biases.

Varying importance of biomarkers across lifespan

The biological markers and processes that influence aging may change as individuals get older. The same markers that predict age well in younger populations might not be as relevant or might behave differently in very old individuals. There are several studies that suggest that tissue changes in our bodies are non-linear in addition to nonlinear DNA methylation patterns (Bell et al., 2019 , Han 2024, Okada et al. 2023, Tian et al. 2023)

Choice of Probes/CpG sites

eAge clocks are trained on data on CpG sites. Methylation at these sties can influence gene expression, thus regulating various biolgical processes. Probes in DNA methylation studies, are DNA fragements that are designed to bind to specific CpG sites. These probes are used in high throughput assays to measure methylation levels at thousands of CpG sites across the genome. Each probe corresponds to a specific CpG site or region. In developing eAge clocks, the choice of which probes to include (and thus CpG) in the model is crucial because it determines how well the clock can predict age. Excluding probes that are not strongly correlated with chronological age might introduce bias because those exclued probes might be relevant for understanding age-related pathology. In short, we might end up with a clock that is great at predicting chronological age, but not so good at predicting biological age. There are other eAge clocks-specific design choices to consider: adjusting for variation in cellular compositon and cutting out probes based on disease status, and low correlation with chronological age are just two examples (Zhang et al., 2019)

As we’ve seen above, the methods for correcting bias depends on the biological source of the data. But there appears to be systematic underestimation of age among older adults in both eAge clocks (El Khoury et al., 2019) and brain age models.

Methods to correct estimation biases

So how do we typically correct for this bias? Anecdotally, from the papers I’ve seen that apply brain age models to study various brain and psychiatric disorders, we typically include chronological age as a covariate into the linear regression model when we’re examining group differences.

Method 1

There are two widely accepted steps to correct for this bias — by either incorporating or excluding chronological age into the correction method. In the first method, chronological age is included in the equation.

First, we subtract the chronological age from the predicted age, which results in brain-predicted age difference (Brain-PAD).

Next we quantify how brain-PAD changes with chronological age by regressing brain-PAD on chronological age. In R, we would fit a model that looks like this mod <- lm(brainpad ~ chronological_age) to obtain the slope and intercept.

We then adjust the predicted age to remove the influence of chronological age. This adjustment ensures that the corrected predicted age reflects the brain’s health independently of the individual’s actual age: corrected_predicted_age <- predicted_age - (beta_1 * chronological_age + beta_0) where beta_0 and beta_1 were obtained from mod above.

Method 2

As an alternative method, we could fit a linear model using the predicted age as the outcome variable instead of the brain-PAD above.

Next, we “correct” beta_1 , which is the slope, without including chronological age into the equation. In this case, the model looks like mod <- lm(predicted_age ~ chronological_age). In other words, the slope here represents how much the predicted age changes with a one-unit change in chronological age, and if there is not a perfect 1:1 match between chronological and predicted age, the model is under- or over-estimating the predicted age. When we do so, we are essentially adjusting the predicted age for the linear relationship between chronological age and predicted age. The operation can be interpreted as transforming the predicted age to account for the discrepancy (which could be positive or negative) between the predicted and chronlogical age.

In this case, we first obtain beta_0 which is obtained from the model by running coef(mod) and then we subtract it from predicted age. The resulting number is then divided by the slope. corrected_predicted_age <- (predicted_age - beta_0) / beta_1.

However, this method could increase the variance in the data as each predicted age is adjusted based on the same regression coefficients regardless of the actual chronological age. This commentary elaborates on the implications of using different correction methods in brain age prediction studies.

What is biological age, anyway?

In sum, addressing estimation bias in age prediction models is crucial for improving the accuracy and clinical relevance of these tools. By understanding the sources of bias, such as noise variability across the lifespan, sample size imbalances, and the specific methods used, researchers can develop more robust models. Correcting for biases using techniques like the incorporation of chronological age as a covariate or adjusting predicted ages through linear regression ensures that these models provide a more accurate picture of aging.

But here’ what is biological age, anyway? Currently, we still lack consensus on what a reliable aging biomarker should comprise, but fret not — initiatives like the Biomakers of Aging Consortium is a step towards systematic development and validation of aging biomarker, including biological clocks. Biological age test kits are increasingly being offered as direct-to-consumer tests; in June 2024, 23andMe announced its Biological Age Feature for its membership subscribers. If we expect to see biological clocks getting more mainstream, it’s imperative to understand the sources of biases depending on the source of the data.

eAge clocks and brain age models are both ML-driven methods to capture the aging process — and they aren’t the only kinds of clocks out there; increasingly, there are clocks trained on other -omics data. These clocks have the potential to transform clinical practice by estimating how much a certain disease is impacting an individual’s biological aging, or who is at risk for developing age-related conditions, paving the way for preventive rather than reactive care. Next time you see a direct-to-consumer biological age test, scrutinize for its biases and how they correct them. Correcting for these biases is crucial to ensure that these models provide an accurate and reliable assessment of biological age, which is essential for practical and actionable lifestyle changes!

References

1. Aycheh, H. M., Seong, J.-K., Shin, J.-H., Na, D. L., Kang, B., Seo, S. W., & Sohn, K.-A. (2018). Biological Brain Age Prediction Using Cortical Thickness Data: A Large Scale Cohort Study. Frontiers in Aging Neuroscience, 10, 252. https://doi.org/10.3389/fnagi.2018.00252
2. Bell, C. G., Lowe, R., Adams, P. D., Baccarelli, A. A., Beck, S., Bell, J. T., Christensen, B. C., Gladyshev, V. N., Heijmans, B. T., Horvath, S., Ideker, T., Issa, J.-P. J., Kelsey, K. T., Marioni, R. E., Reik, W., Relton, C. L., Schalkwyk, L. C., Teschendorff, A. E., Wagner, W., … Rakyan, V. K. (2019). DNA methylation aging clocks: Challenges and recommendations. Genome Biology, 20(1), 249. https://doi.org/10.1186/s13059-019-1824-y
3. Cole, J. H., Poudel, R. P. K., Tsagkrasoulis, D., Caan, M. W. A., Steves, C., Spector, T. D., & Montana, G. (2017). Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker. NeuroImage, 163, 115–124. https://doi.org/10.1016/j.neuroimage.2017.07.059
4. de Lange, A.-M. G., & Cole, J. H. (2020). Commentary: Correction procedures in brain-age prediction. NeuroImage : Clinical, 26, 102229. https://doi.org/10.1016/j.nicl.2020.102229
5. El Khoury, L. Y., Gorrie-Stone, T., Smart, M., Hughes, A., Bao, Y., Andrayas, A., Burrage, J., Hannon, E., Kumari, M., Mill, J., & Schalkwyk, L. C. (2019). Systematic underestimation of the epigenetic clock and age acceleration in older subjects. Genome Biology, 20(1), 283. https://doi.org/10.1186/s13059-019-1810-
6. Franke, K., Ziegler, G., Klöppel, S., & Gaser, C. (2010). Estimating the age of healthy subjects from T1-weighted MRI scans using kernel methods: Exploring the influence of various parameters. NeuroImage, 50(3), 883–892. https://doi.org/10.1016/j.neuroimage.2010.01.005
7. Han, J.-D. J. (2024). The ticking of aging clocks. Trends in Endocrinology & Metabolism, 35(1), 11–22. https://doi.org/10.1016/j.tem.2023.09.007
8. Hannum, G., Guinney, J., Zhao, L., Zhang, L., Hughes, G., Sadda, S., Klotzle, B., Bibikova, M., Fan, J.-B., Gao, Y., Deconde, R., Chen, M., Rajapakse, I., Friend, S., Ideker, T., & Zhang, K. (2013). Genome-wide Methylation Profiles Reveal Quantitative Views of Human Aging Rates. Molecular Cell, 49(2), 359–367. https://doi.org/10.1016/j.molcel.2012.10.016
9. Horvath, S. (2013). DNA methylation age of human tissues and cell types. Genome Biology, 14(10), 3156. https://doi.org/10.1186/gb-2013-14-10-r115
10. Liang, H., Zhang, F., & Niu, X. (2019). Investigating systematic bias in brain age estimation with application to post‐traumatic stress disorders. Human Brain Mapping, 40(11), 3143–3152. https://doi.org/10.1002/hbm.24588
11. Okada, D., Cheng, J. H., Zheng, C., Kumaki, T., & Yamada, R. (2023). Data-driven identification and classification of nonlinear aging patterns reveals the landscape of associations between DNA methylation and aging. Human Genomics, 17(1), 8. https://doi.org/10.1186/s40246-023-00453-z
12. Pardoe, H. R., & Kuzniecky, R. (2018). NAPR: A Cloud-Based Framework for Neuroanatomical Age Prediction. Neuroinformatics, 16(1), 43–49. https://doi.org/10.1007/s12021-017-9346-9
13. Tian, Y. E., Cropley, V., Maier, A. B., Lautenschlager, N. T., Breakspear, M., & Zalesky, A. (2023). Heterogeneous aging across multiple organ systems and prediction of chronic disease and mortality. Nature Medicine, 29(5), 1221–1231. https://doi.org/10.1038/s41591-023-02296-6
14. Zhang, Q., Vallerga, C. L., Walker, R. M., Lin, T., Henders, A. K., Montgomery, G. W., He, J., Fan, D., Fowdar, J., Kennedy, M., Pitcher, T., Pearson, J., Halliday, G., Kwok, J. B., Hickie, I., Lewis, S., Anderson, T., Silburn, P. A., Mellick, G. D., … Visscher, P. M. (2019). Improved precision of epigenetic clock estimates across tissues and its implication for biological ageing. Genome Medicine, 11. https://doi.org/10.1186/s13073-019-0667-1